Coding The Matrix: Linear Algebra Through Computer Science Applications

Sign up for updates

• To receive messages when new material is available, e.g. blog posts about applications of linear algebra to CS, news of a follow-on course, or corrections to the book, join the mailing list. I promise that mailings will be rare and that I will not share your email address with anybody, ever.

  Email Address: Subscribe Unsubscribe

About The Book

• Edition 1 of the textbook is available for purchase. It incorporates corrections and a revised and expanded index. List Price: $35.00  Publisher: Newtonian Press Purchase in UK Purchase in Germany Errata for Edition 1 Here is  a revised and expanded index for Edition 0. Send mail if you have questions about using the book for a university course.

Example Applications

Here are examples of applications addressed in Coding the Matrix.

• 
  

• crossfade

  
  
  A line segment between points is given by the convex combinations of those points; if the "points" are images, the line segment is a simple morph between the images.
  

• Perspective rectification

  
  
  Given a photo of a whiteboard taken at an angle, synthesize a perspective-free view of the whiteboard. 
  
  
   
  
  The same transformation can be used in using a Wiimote to make a low-cost interactive whiteboard or light pen (due to Johnny Chung Lee).
  

• Error-correcting codes
  
  
  
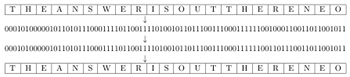
  Error-correcting codes are used, e.g., by cellphones to preserve data transmitted over a noisy channel while maintaining high throughput.
  

• Integer factorization
  
  522253825433285668885771662040104167 = 891428822186035241∙585861498344390287
  
  
  Factoring an integer is a hard computational problem (and the RSA cryptosystem depends on it being hard).  At the core of the most sophisticated integer-factoring algorithms is a simple problem in linear algebra.

• Image blurring

  
  
  Blurring an image is a simple linear transformation.
  

• Searching within an audio clip

  
  
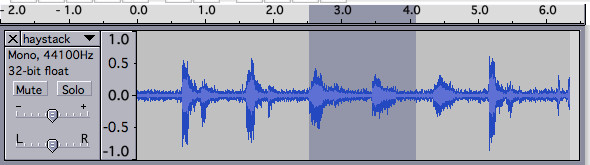
  Searching for one audio clip within another can be formulated as a convolution.  A convolution can be computed very quickly using the Fast Fourier Transform.
  

• Searching within an image
  
   
  
  Convolution can also be done in two dimensions, enabling one to quickly search for a subimage within an image.
  

• Audio and image compression
  
  Compression of audio and images aids efficient storage and transmission.  Lossy compression techniques such as those used in MP3 (audio) and JPEG (images) are based in part on linear algebra,
  e.g. wavelet transform and Fourier transform.
  

  100% original size

  40% original size

  10% original size

• Face detection

  
  
  A "classical" approach to face detection is eigenfaces, a technique related to principal component analysis.
  

• 2d graphics transformations

  
  
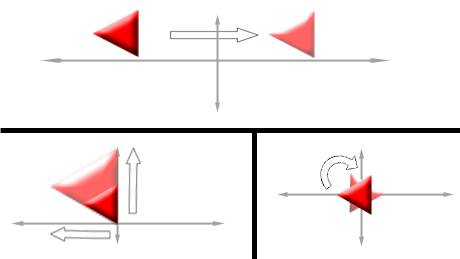
  Simple transformations that arise in graphics such as rotation, translation, and scaling can be expressed using matrices.
  

• Lights Out

  
  
  Lights Out is a puzzle in which you must select the correct buttons to push in order for all the lights to go out.  Finding a solution can be expressed as a problem in linear algebra.
  

• Minimum-weight spanning forest

  
  
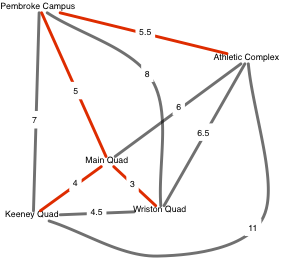
  Finding the minimum-weight spanning tree of a graph can be interpreted as the problem of finding a minimum-weight basis for a vector space
  derived from the graph.
  

• Graph layout

  
  
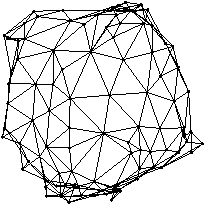
  A nice drawing of a graph can be obtained from eigenvectors of a related matrix.